Caros Leitores;
diyun Zhu/Getty Images
A descoberta inesperada de uma fase geométrica mostra como a matemática e a física estão intimamente interligadas.
Eu não achava matemática particularmente emocionante quando estava no ensino médio. Para ser honesto, eu só estudei quando fui para a universidade porque inicialmente parecia bem fácil para mim. Mas na minha primeira aula de matemática como estudante de graduação, percebi que tudo o que eu achava que sabia sobre matemática estava errado. Era tudo menos fácil. Matemática, eu logo descobri, pode ser realmente emocionante — especialmente se você for além do reino da aritmética pura.
Na física, o conteúdo realmente surpreendente — conceitos que vão contra sua intuição sobre o Universo — surge por volta do ensino médio, quando os alunos podem vislumbrar o estranho mundo quântico e encontrar as teorias da relatividade geral e especial de Einstein. A matemática escolar não consegue acompanhar essas maravilhas. Você aprende operações aritméticas elementares, integração e derivação, o manuseio básico de probabilidades e vetores. Se você tiver sorte, professores ambiciosos podem mostrar uma prova simples. E é isso. Então não é de se admirar que muitos alunos não consigam desenvolver uma paixão real pelo assunto.
No entanto, a matemática oferece todos os tipos de surpresas, como o paradoxo de Banach-Tarski , que afirma que você pode dobrar uma esfera quase magicamente, ou o fato de que há infinitamente muitos infinitos diferentes . O que realmente me surpreendeu foi descobrir o quão profundamente a matemática está entrelaçada com os fenômenos físicos mais estranhos. Não é necessariamente a física quântica em si que dá origem aos efeitos incríveis; não, os sistemas sempre seguem as regras estritas da matemática. Como o químico Peter Atkins colocou em seu livro de 2003 Galileo's Finger , "Determinar onde a matemática termina e a ciência começa é tão difícil e inútil quanto mapear a borda de uma névoa matinal".
Poucos exemplos ilustram a mistura de matemática e física melhor do que uma descoberta feita pelo físico Michael Berry. Em 1984, Berry revelou um lado geométrico profundo e amplamente inesperado da mecânica quântica . Essa geometria, Berry percebeu, dá às partículas quânticas um tipo de memória.
Nada deveria realmente acontecer
Na época, Berry estava investigando um sistema muito simples: o estado quântico de uma partícula, como um nêutron, em um ambiente em mudança. Os nêutrons têm uma propriedade quântica chamada spin, que age como um pequeno ímã que as partículas carregam consigo. Esse spin pode ser orientado com o polo norte voltado para cima ou para baixo — então os físicos falam de nêutrons tendo "spin up" ou "spin down". O spin de um nêutron é influenciado por campos magnéticos externos.
Berry usou meios matemáticos para investigar o que aconteceria com o nêutron se a direção do campo magnético mudasse lentamente. De acordo com o chamado teorema adiabático, que foi introduzido no início do século XX, as propriedades quânticas da partícula não deveriam mudar como resultado: sua energia, momento, massa e spin permanecem os mesmos.
Se você lentamente girar a direção do campo magnético e então movê-lo de volta para a direção original, essa ação não deveria, em princípio, mudar nada. “Essa, de qualquer forma, foi a opinião predominante entre os físicos por muitos anos”, escreveu Berry em um artigo na Scientific American em dezembro de 1988. Mas uma “mudança na fase de uma função de onda foi esquecida”.
Um dos fenômenos mais estranhos da mecânica quântica é a dualidade onda-partícula: objetos quânticos podem ser imaginados como formas pontuais, mas eles também exibem comportamento de onda como água. Uma fase descreve um deslocamento da onda por um certo ângulo — por exemplo, a função cosseno nada mais é do que uma função seno deslocada em fase.
Como Berry reconheceu em seus cálculos, uma mudança lenta no campo magnético faz com que a função de onda do nêutron gire em uma certa fase. Isso significa que a função de onda da partícula mostra o que aconteceu no passado (nesse caso, a mudança no campo magnético). Além disso, Berry reconheceu que essa fase não ocorre apenas no caso especial de uma partícula em um campo magnético. Várias situações nas quais um sistema quântico é lentamente alterado e então retornado às suas condições originais deixam rastros na função de onda.
Experimentos conduzidos logo após a publicação do trabalho inovador de Berry confirmaram essas ideias. Se você está familiarizado com a mecânica quântica, então provavelmente sabe que a função de onda não é uma quantidade diretamente observável. No entanto, há uma maneira de medir a mudança de fase usando uma segunda partícula como referência. Nesses experimentos, os físicos permitiram a colisão de duas partículas, como nêutrons, uma das quais estava anteriormente em um campo magnético variável. Quando os nêutrons se encontraram, suas funções de onda interagiram.
Essas funções se comportam como ondas de água: se os vales e picos se alinham, eles se fortalecem; se, por outro lado, eles são deslocados um contra o outro, eles podem enfraquecer ou morrer completamente. Esses fenômenos são conhecidos como interferência construtiva ou destrutiva, respectivamente.
Os experimentos revelaram que Berry estava certo: os nêutrons estavam fora de fase, interferindo destrutivamente. Essa observação indicou que uma das partículas esteve brevemente em um campo magnético mutável. Embora nenhuma de suas propriedades mensuráveis tenha mudado diretamente como resultado, sua função de onda alterada o denunciou.
O Universo Curvo
Mas como Berry sabia que as partículas passariam por uma mudança de fase? Na verdade, tal fase aparece onde quer que haja curvatura. É por isso que a fase desempenha um papel importante na teoria geral da relatividade de Einstein — a teoria que ele usou para descrever a gravidade.
Alguns especialistas afirmam que a relatividade geral é mais geometria do que física. De acordo com essa teoria, a matéria curva o espaço-tempo, e essa deformação faz com que as massas se atraiam — um fenômeno que percebemos como gravidade. Gosto de pensar nisso como uma folha de borracha na qual objetos pesados são colocados, deformando a folha e, portanto, influenciando os objetos. Essa visualização tem algumas fraquezas, no entanto: o espaço-tempo é bidimensional nessa concepção, e eu o olho de cima para baixo do meu mundo tridimensional. A relatividade geral, por outro lado, descreve a curvatura do espaço-tempo quadridimensional sem olhar para ele de uma perspectiva pentadimensional.
Isso levanta a questão de como você pode deduzir a curvatura de algo se não pode olhar para o objeto de fora. A fase que Berry observou ajuda aqui.
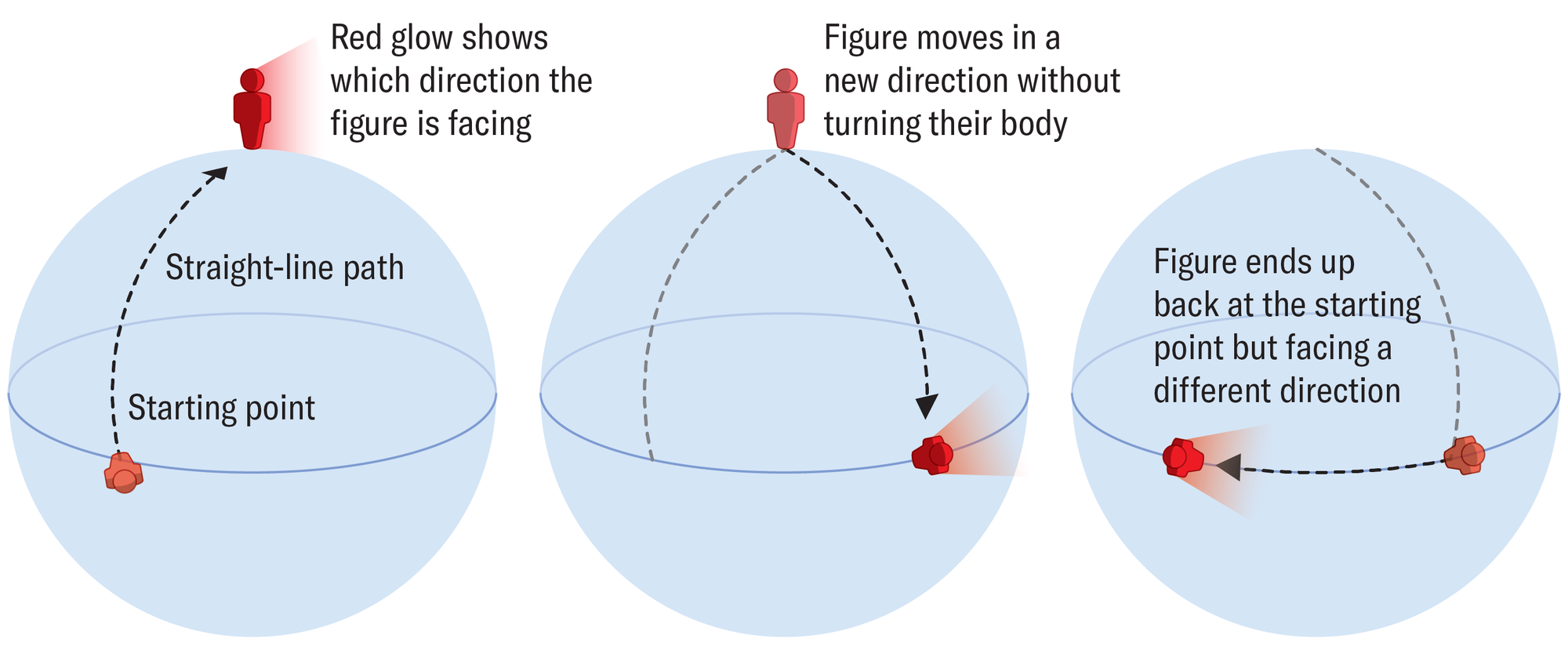
Suponha que eu quisesse provar de uma forma complicada que a Terra é uma esfera. Para fazer isso, eu posso andar direto para o norte a partir da minha localização em algum lugar na Alemanha sobre montanhas, vales, rios, lagos e oceanos. Neste experimento mental, nada pode me impedir de seguir um caminho reto. Quando chego ao Polo Norte, eu me movo para a direita sem me virar, andando de lado como um caranguejo. Eu caminho até chegar na mesma latitude de onde comecei. Então sigo a latitude para a esquerda — novamente sem me virar — até chegar de volta ao ponto de partida. Embora eu pouse no meu lugar original, eu não olho mais para o norte, como fiz no começo, mas para o leste. Então esta viagem de ida e volta não me mudou como pessoa (exceto talvez pelo esforço físico), mas eu virei em um certo ângulo.
Amanda Montañez
Se eu tivesse seguido o mesmo caminho em um plano plano, eu teria retornado ao ponto de partida sem nenhuma rotação. Mas neste experimento mental, ambientado em nosso planeta curvo, a mesma coisa acontece comigo quanto à função de onda na teoria de Berry: ela recebe uma fase, um ângulo que a desloca.
O ângulo que peguei durante minhas viagens depende unicamente da geometria da Terra. Seu valor é proporcional à área delimitada pelo meu caminho. Como nada mais influencia a fase — nem minha velocidade nem se eu faço uma pausa — ela é chamada de “fase geométrica”.
Para os matemáticos, isso não era novidade na época em que Berry publicou seu trabalho. Eles sabiam do conceito há muitas décadas. Mas ninguém havia aplicado fases geométricas a processos mecânico-quânticos. A fase na função de onda revela a geometria do chamado espaço de parâmetros. Este é um espaço abstrato de alta dimensão que combina todos os parâmetros que podem influenciar a função de onda (como campo magnético, energia, localização e velocidade). A mudança de curto prazo na direção de um campo magnético (ou outro parâmetro) descreve uma curva fechada neste espaço — assim como meu caminho circular no globo. Como esse espaço de parâmetros geralmente é curvo, isso deixa rastros na função de onda.
“A fase geométrica pode, portanto, ser considerada a melhor resposta que o sistema pode oferecer à questão 'Qual caminho no espaço de parâmetros o sistema tomou?” Berry escreveu em seu artigo de 1988 na Scientific American . “Nesse sentido, é um tipo de 'memória' quântica.”
Berry havia, assim, revelado uma profunda conexão entre sistemas quânticos e geometria, que se mostrou extremamente valiosa. A fase de Berry, nomeada em sua homenagem, pode ser usada para explicar fenômenos como o efeito Hall quântico , que ocorre em certos sólidos e levantou muitas questões antes da descoberta de Berry.
Tudo isso é extremamente emocionante. Para mim, no entanto, o mais impressionante é que Berry estabeleceu o novo campo de pesquisa da física quântica geométrica ao se basear em conceitos matemáticos existentes. Ele não precisou adicionar nada de novo à física ou à matemática — em vez disso, a matemática tornou possível revelar algo completamente inesperado na física.
Este artigo foi publicado originalmente no Spektrum der Wissenschaft e foi reproduzido com permissão.
Manon Bischoff é física teórica e editora da Spektrum , uma publicação parceira da Scientific American .
Para saber mais, acesse o link>
Fonte: Scientific American Por Manon Bischoff
https://www.scientificamerican.com/article/how-geometry-revealed-quantum-memory/
=======================
Acesse, o link da Livraria> https://www.orionbook.com.br/
Page: http://econo-economia.blogspot.com
Page: http://pesqciencias.blogspot.com.br
Page: http://livroseducacionais.blogspot.com.br
e-mail: heliocabral@coseno.com.br
e-mail: cabralhelio@hotmail.com


Nenhum comentário:
Postar um comentário